Digital Data
In a CD (and any other digital recording technology), the goal is to create a recording with very high fidelity (very high similarity between the original signal and the reproduced signal) and perfect reproduction (the recording sounds the same every single time you play it no matter how many times you play it).
To accomplish these two goals, digital recording converts the analog wave into a stream of numbers and records the numbers instead of the wave. The conversion is done by a device called an analog-to-digital converter (ADC). To play back the music, the stream of numbers is converted back to an analog wave by a digital-to-analog converter (DAC). The analog wave produced by the DAC is amplified and fed to the speakers to produce the sound.
The analog wave produced by the DAC will be the same every time, as long as the numbers are not corrupted. The analog wave produced by the DAC will also be very similar to the original analog wave if the analog-to-digital converter sampled at a high rate and produced accurate numbers.
You can understand why CDs have such high fidelity if you understand the analog-to-digital conversion process better. Let's say you have a sound wave, and you wish to sample it with an ADC. Here is a typical wave (assume here that each tick on the horizontal axis represents one-thousandth of a second):
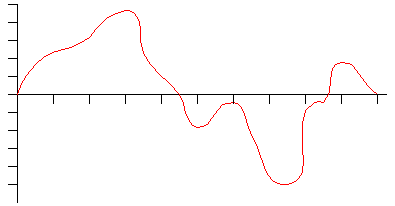
When you sample the wave with an analog-to-digital converter, you have control over two variables:
The sampling rate - Controls how many samples are taken per second
The sampling precision - Controls how many different gradations (quantization levels) are possible when taking the sample
In the following figure, let's assume that the sampling rate is 1,000 per second and the precision is 10:
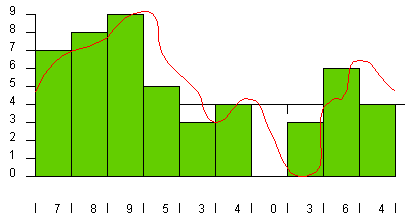
The green rectangles represent samples. Every one-thousandth of a second, the ADC looks at the wave and picks the closest number between 0 and 9. The number chosen is shown along the bottom of the figure. These numbers are a digital representation of the original wave. When the DAC recreates the wave from these numbers, you get the blue line shown in the following figure:
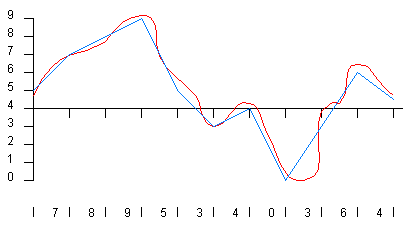
You can see that the blue line lost quite a bit of the detail originally found in the red line, and that means the fidelity of the reproduced wave is not very good. This is the sampling error. You reduce sampling error by increasing both the sampling rate and the precision. In the following figure, both the rate and the precision have been improved by a factor of 2 (20 gradations at a rate of 2,000 samples per second):
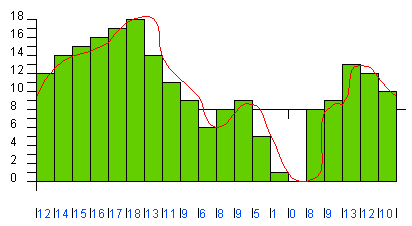
In the following figure, the rate and the precision have been doubled again (40 gradations at 4,000 samples per second):
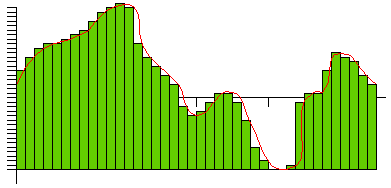
You can see that as the rate and precision increase, the fidelity (the similarity between the original wave and the DAC's output) improves. In the case of CD sound, fidelity is an important goal, so the sampling rate is 44,100 samples per second and the number of gradations is 65,536. At this level, the output of the DAC so closely matches the original waveform that the sound is essentially "perfect" to most human ears.
Thanks to MattD for the following [DM]:
Bit depth and sample rate are two different things.
Sample rate deals with the time/frequency domain. The more samples per second, the more time-accurate the recorded data is. Higher sample rates tend to image better for this reason (compare 24/48 to 24/96 to see).
Bit depth has to do with amplitude. Each bit can either be a 0 or a 1. This process occurs x times a second (where x is the sample rate). For 16-bit data, each of those 16 bits can either be a 0 or a 1, yielding 2^16 or 65,536 possible ways of representing a sample. Furthermore, each bit represents about 6 dB of audio, so 16-bit audio has a maximum theoretical dynamic range of 6*16 = 96 dB.
On the other hand, each 24-bit audio sample can be represented in 2^24 or 16,777,216 different ways and has a theoretical maximum dynamic range of 6*24 = 144 dB.
Bit depth and sample rate are independent of each other. The reason that people do not record 16/96 and such is that high frequency information is typically at much lower levels than the main part of the signal. On a 16-bit AD, this would be near the theoretical bottom of the dynamic range (for example, I have 24/96 recordings that have information from 20-30 kHz at about -80 dB.